H29　中央大杉並高等学校(推薦)　数学講評

大問１　文字式の計算

通分とマイナスの処理、それぞれ丁寧に行いましょう。

大問２　資料の活用

数え間違えに気を付けるだけですね。
問題ないと思います。

大問３　平面図形

動点に相似が絡んだ問題です。
三平方を使ってもいいですが、(1:2:ルート3の直角三角形ですね)
相似だけで解いた方がスマートかもしれません。

ピックアップ１題！

AB＝５√３、BC＝５、CA＝１０の直角三角形がある。
点Pは、秒速１cmで辺上をCからAまで動きます。
点Qは点Pと同時に出発して、秒速１cmで辺上をBからCまで動きます。
直線PQが辺ABに平行になるとき、△AQPの面積を求めなさい。

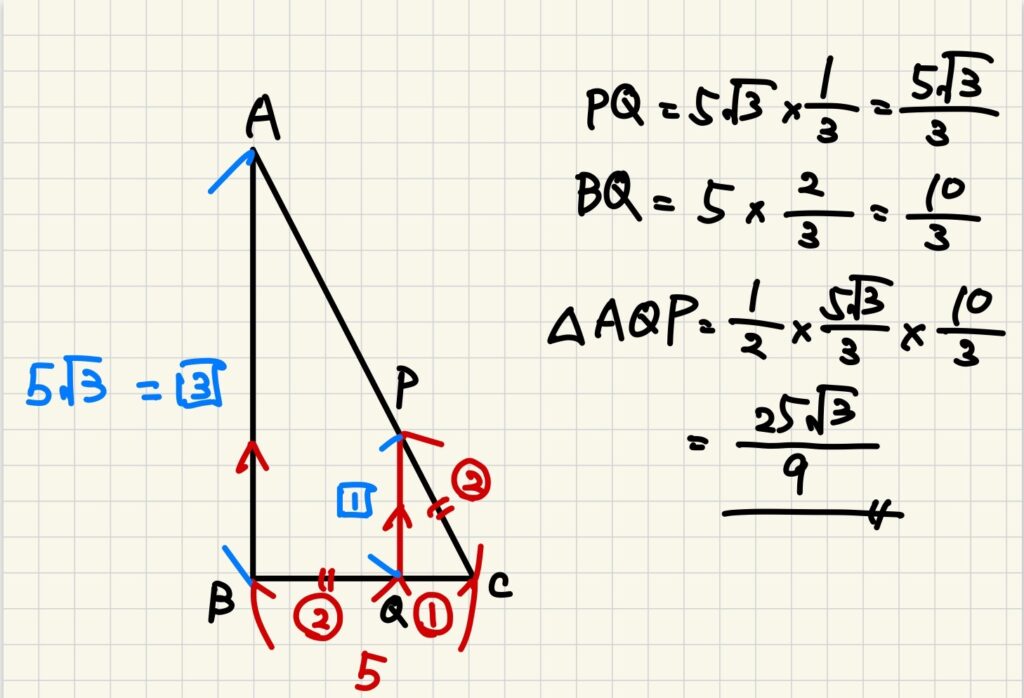
△ABC∽△PQCより、PC:PQ=２:１と分かりますね。
PC＝BQですからBQ:QCが２:１となり、△ABCと△PQCの相似比が３:１となります。
あとは底辺PQと高さBQを出して面積を求めましょう。(下図参照。)

大問４　関数

y=kをそれぞれ代入して点A、点Cのx座標を求めれば、点Bのx座標をkを用いて表すことができますね。
あとは式に代入してaを求めましょう。

大問５　平面図形

円の直径からEFの長さがすぐに分かりますが、長方形EFGHは正方形ではないので注意しましょう。
EHの長さは補助線を入れることで求められますね。

まとめ

大問２、大問５辺りで差がつきそうです。
ただこのレベルであれば満点を狙いたいですね。